Download top and best high-quality free Triangle PNG Transparent Images backgrounds available in various sizes. To view the full PNG size resolution click on any of the below image thumbnail.

License Info: Creative Commons 4.0 BY-NC

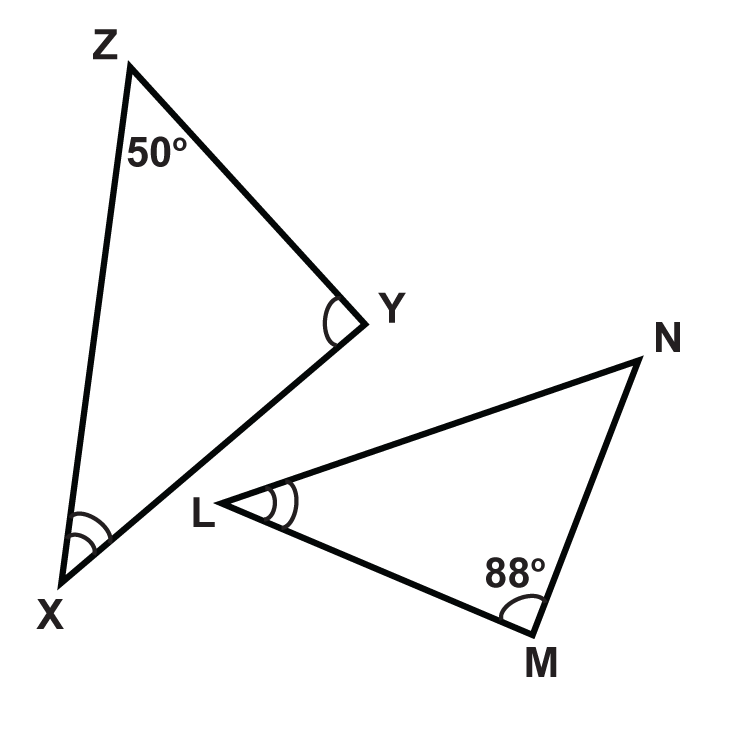
A triangle is a three-sided polygon with three vertices and three edges. It is one of the most fundamental geometric forms. Triangle ABC is a triangle with vertices A, B, and C.

In Euclidean geometry, any three non-collinear points form a unique triangle and, at the same time, a unique plane (i.e. a two-dimensional Euclidean space). In other words, the triangle is contained in just one plane, and every triangle is contained in some plane. There is only one plane and all triangles are enclosed in it if the entire geometry is the Euclidean plane; however, this is no longer true in higher-dimensional Euclidean spaces. Except when otherwise specified, this article is about triangles in Euclidean geometry, specifically the Euclidean plane.

Triangle classification terminology dates back over two thousand years, having been defined on the first page of Euclid’s Elements. Modern categorization names are either straight transliterations of Euclid’s Greek or Latin translations of those designations.

According to the lengths of their sides, ancient Greek mathematician Euclid identified three sorts of triangles:

‘Of trilateral figures, an isopleuron triangle has three equal sides, an isosceles triangle has two equal sides, and a scalene triangle has three unequal sides.’

Three sides of an equilateral triangle are the same length. A regular polygon with all angles measuring 60 degrees is an equilateral triangle.

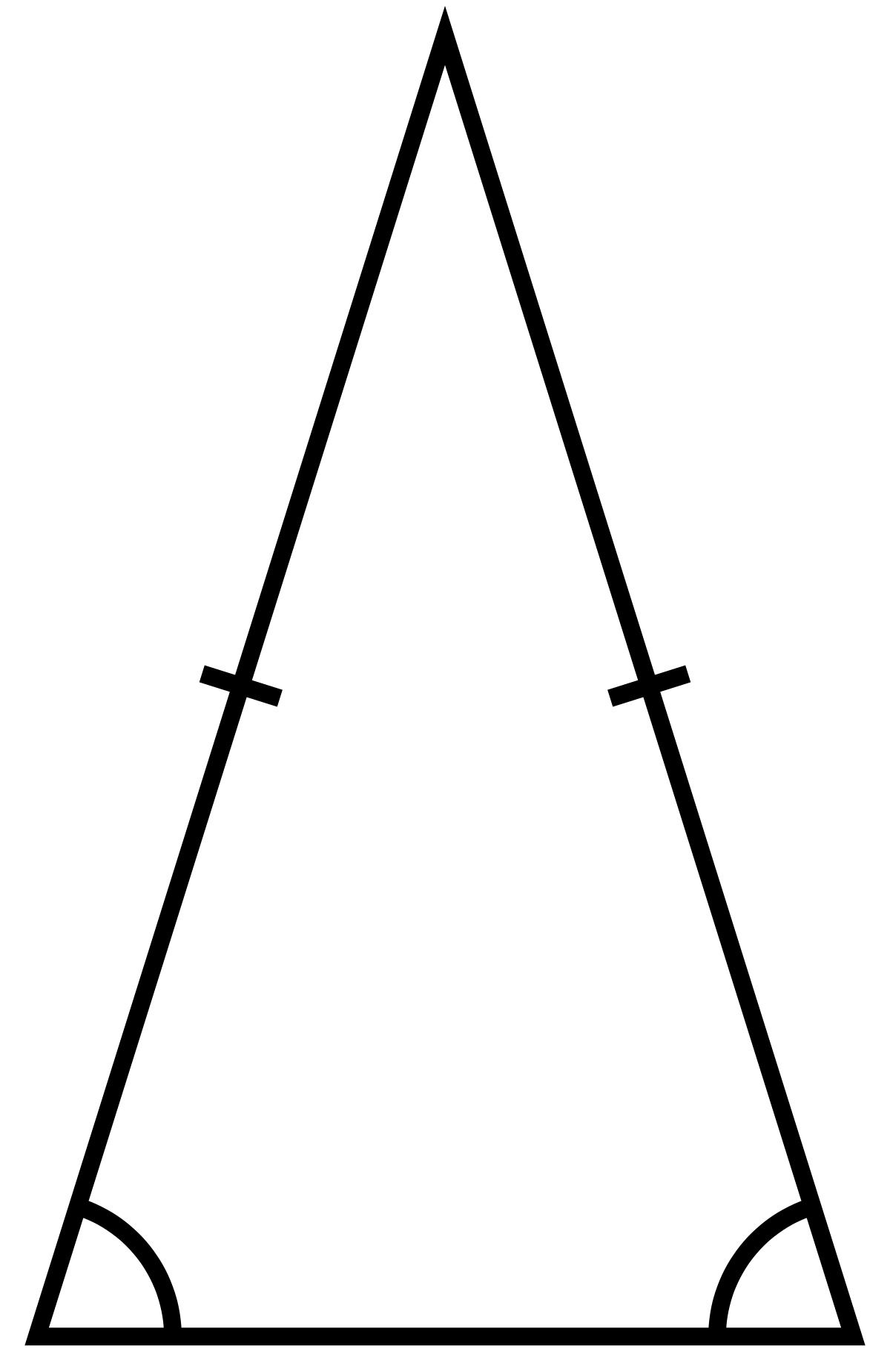
Two sides of an isosceles triangle are of equal length. In addition, an isosceles triangle has two angles of equal length, namely the angles opposing the two sides of equal length. The isosceles triangle theorem, which Euclid was aware of, is based on this fact. An isosceles triangle is defined by some mathematicians as having exactly two equal sides, while others describe it as having at least two equal sides. According to the latter definition, all equilateral triangles are isosceles triangles. Isosceles is the 45″45″90 right triangle that appears in the tetrakis square tiling.

All of the sides of a scalene triangle are different lengths. It has all angles of different measures in the same way.

Hatch markings, sometimes known as tick marks, are used to denote equal-length sides in diagrams of triangles and other geometric forms. A side can be marked with a pattern of “ticks,” or small line segments in the form of tally marks; if both sides are marked with the same pattern, they are of equal length. The pattern in a triangle is generally no more than three ticks. An equilateral triangle has the same pattern on all three sides, whereas an isosceles triangle has the same pattern on just two sides. A scalene triangle, on the other hand, has distinct patterns on all three sides since no sides are equal.

Similarly, inside the angles, patterns of 1, 2, or 3 concentric arcs are used to indicate equal angles: an equilateral triangle has the same pattern on all three angles, an isosceles triangle has the same pattern on only two angles, and a scalene triangle has different patterns on all angles, because no angles are equal.

By Means of Internal Angles

The “definitions” part of Book I of Euclid’s Elements, as seen on the first page of the world’s first printed version (1482). “Orthogonius” is the name of the right triangle, while “acutus” and “angulus obtusus” are the names of the two angles represented.

Internal angles, which are measured in degrees, can also be used to classify triangles.

One of the internal angles of a right triangle (or right-angled triangle, historically known as a rectangled triangle) is 90 degrees (a right angle). The hypotenuse, or longest side of the triangle, is the side opposite the right angle. The triangle’s legs, or catheti (singular: cathetus), are the other two sides. The Pythagorean theorem states that the sum of the squares of the lengths of the two legs equals the square of the hypotenuse length: a2 + b2 = c2, where a and b are the leg lengths and c is the hypotenuse length. Special right triangles have special qualities that make computations using them easier. The 3″4″5 right triangle, in which 32 + 42 = 52, is one of the two most well-known. The numbers 3, 4, and 5 form a Pythagorean triple in this case. The other is an isosceles triangle (45″45″90 triangle), which has two 45-degree angles.

An acute triangle, also known as an acute-angled triangle, is a triangle having all internal angles smaller than 90 degrees. If c is the longest side’s length, then a2 + b2 > c2, where a and b are the other sides’ lengths.

An obtuse triangle, also known as an obtuse-angled triangle, is a triangle having one internal angle greater than 90 degrees. If c is the longest side’s length, then a2 + b2 = c2, where a and b are the other sides’ lengths.

Degenerate is a triangle having an internal angle of 180° (and collinear vertices). The vertices of a right degenerate triangle are collinear, with two of them being coinciding.

Isosceles triangles have two angles with the same measure as well as two sides with the same length. As a result, in a triangle with the same measure of all angles, all three sides have the same length, and the triangle is equilateral.

Download Triangle PNG images transparent gallery.